Why Planes Don’t Fly in Straight Lines

When we think about the shortest distance between two points, most of us recall a basic lesson from school: it’s a straight line. While that holds true in flat, Euclidean geometry, the reality of air travel on our spherical Earth tells a different story. Planes don’t fly in straight lines—they follow curved paths called geodesics or great circle routes. Let’s dive into why this happens and explore a real-world example.

The Geometry of a Spherical Earth

Earth isn’t flat (sorry, flat-earthers!). It’s an oblate spheroid, and this shape fundamentally changes how we calculate the shortest path between two locations. On a flat surface, a straight line is the quickest way to get from point A to point B. But on a sphere, the shortest path is a geodesic, a segment of a great circle—an imaginary circle on the Earth’s surface that shares the same center as the planet itself.

Think of a great circle as the largest possible circle you can draw on a globe, like the equator or a meridian line that passes through both poles. These paths curve when viewed on a flat map, but they’re the most efficient routes for long-distance travel, minimizing distance and, often, fuel consumption.

Why Do Flight Paths Look Curved?

When you look at a flight route on a flat map—like the ones on in-flight entertainment screens or tracking apps—the path often appears to curve dramatically. This is because flat maps distort the three-dimensional reality of Earth’s surface. The most common map projection, the Mercator projection, stretches the globe onto a flat plane, making areas near the poles (like the Arctic) appear much larger than they are. As a result, a geodesic path that’s perfectly “straight” on a globe looks like an arc on a Mercator map.

This curvature isn’t just a visual quirk—it’s a practical necessity. Airlines use great circle routes to save time, fuel, and money. By following the Earth’s curvature, planes take the shortest possible path, even if it looks odd on a flat map.

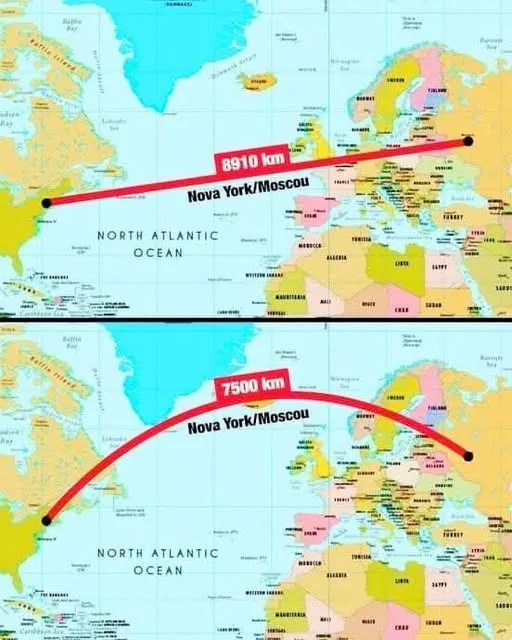
A Real-World Example: New York to Moscow

Let’s take a concrete example: a flight from New York (JFK) to Moscow (SVO). If you were to draw a straight line between these two cities on a flat world map, you might expect the plane to fly directly across the Atlantic Ocean, passing over parts of Western Europe. But that’s not what happens.

Instead, the flight follows a great circle route, which arcs northward. A typical flight path might take the plane over Newfoundland, the Atlantic Ocean, southern Greenland, Iceland, and Scandinavia before descending into Moscow. On a flat map, this looks like a dramatic northward curve, but on a globe, it’s the shortest distance—roughly 7,500 km (4,660 miles).

Why the northward arc? Because the Earth’s spherical shape makes the path over the polar regions shorter than a “straight” line across the mid-latitudes. This route shaves off hundreds of kilometers compared to a flat-map-inspired path, saving fuel and reducing flight time.

Other Factors Influencing Flight Paths

While geodesics are the foundation of flight planning, other factors can tweak the actual route a plane takes:

• Jet Streams: These high-altitude air currents can speed up or slow down a flight. Pilots often adjust routes to ride favorable jet streams or avoid headwinds.

• Airspace Restrictions: Political boundaries, military zones, or conflict areas can force planes to deviate from the ideal great circle route.

• Weather: Storms or turbulence may require pilots to take a slightly longer path for safety.

• Air Traffic Control: Congested airspace or airport scheduling can influence the exact trajectory.

Despite these adjustments, the great circle route remains the starting point for most long-haul flight plans.

Visualizing the Great Circle

To better understand this concept, imagine stretching a piece of string between two points on a globe—say, New York and Moscow. The string naturally follows the Earth’s curvature, forming a great circle path. If you then flatten that globe into a map, the string’s path appears curved. This is why flight-tracking apps like FlightRadar24 show those arcing routes—they’re simply reflecting the reality of spherical geometry.

If you’re curious to explore this yourself, online tools like the Great Circle Mapper (gcmap.com) let you plot flight paths and see how they curve across the globe. It’s a fascinating way to visualize how airlines navigate our planet.

Conclusion

The next time you’re on a long-haul flight and notice the route curving on the in-flight map, you’ll know why. Planes don’t fly in straight lines because Earth isn’t flat—it’s a sphere, and the shortest path follows a geodesic or great circle route. This principle, rooted in the geometry of our planet, ensures flights like New York to Moscow are as efficient as possible. So, the next time you’re soaring through the skies, take a moment to appreciate the elegant math guiding your journey!